路径总和 III

题目描述

给定一个二叉树的根节点 root，和一个整数 targetSum，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

示例 1：
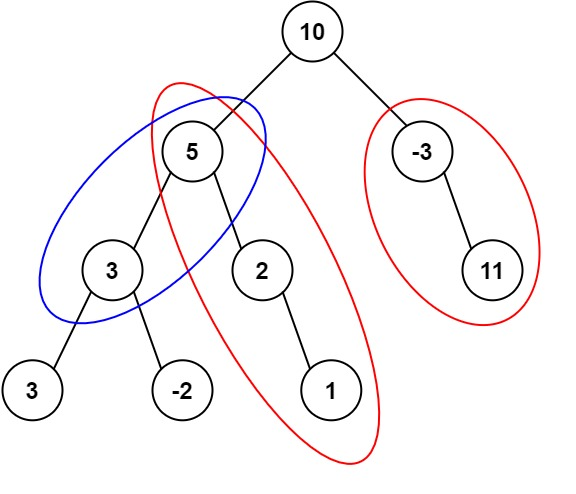
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2： 输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

思路&js代码

1、深度优先搜索

var pathSum = function(root, targetSum) {
    if (root == null) {
        return 0;
    }
    
    let ret = rootSum(root, targetSum);
    ret += pathSum(root.left, targetSum);
    ret += pathSum(root.right, targetSum);
    return ret;
};
 
const rootSum = (root, targetSum) => {
    let ret = 0;
 
    if (root == null) {
        return 0;
    }
    const val = root.val;
    if (val === targetSum) {
        ret++;
    } 
 
    ret += rootSum(root.left, targetSum - val);
    ret += rootSum(root.right, targetSum - val);
    return ret;
}

2、前缀和

var pathSum = function(root, targetSum) {
    const prefix = new Map();
    prefix.set(0, 1);
    return dfs(root, prefix, 0, targetSum);
}
 
const dfs = (root, prefix, curr, targetSum) => {
    if (root == null) {
        return 0;
    }
 
    let ret = 0;
    curr += root.val;
 
    ret = prefix.get(curr - targetSum) || 0;
    prefix.set(curr, (prefix.get(curr) || 0) + 1);
    ret += dfs(root.left, prefix, curr, targetSum);
    ret += dfs(root.right, prefix, curr, targetSum);
    prefix.set(curr, (prefix.get(curr) || 0) - 1);
 
    return ret;
}