题目描述
给定 n 个非负整数,用来表示柱状图中各个柱子的高度。每个柱子彼此相邻,且宽度为 1。
求在该柱状图中,能够勾勒出来的矩形的最大面积。
示例 1:
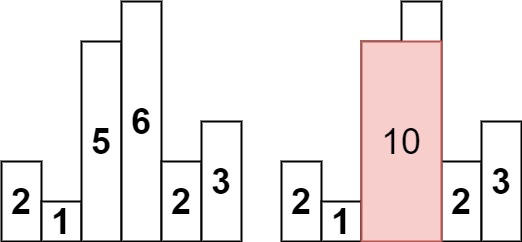
输入:heights = [2,1,5,6,2,3]
输出:10
解释:最大的矩形为图中红色区域,面积为 10
示例 2:
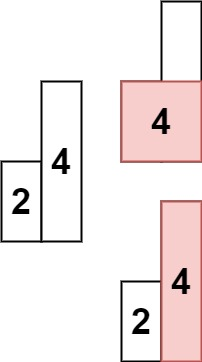
输入:heights = [2,4]
输出:4
思路&js代码
1、单调栈,三次遍历
首先,面积最大矩形的高度一定是 heights 中的元素。这可以用反证法证明:假如高度不在 heights 中,比如 4,那我们可以增加高度直到触及某根柱子的顶部,比如增加到 5,由于矩形底边长不变,高度增加,我们得到了面积更大的矩形,矛盾,所以面积最大矩形的高度一定是 heights 中的元素。
假设 h=heights[i] 是矩形的高度,那么矩形的宽度最大是多少?我们需要知道:
- 在 i 左侧的小于 h 的最近元素的下标 left,如果不存在则为 −1。求出了 left,那么 left+1 就是矩形最左边那根柱子。
- 在 i 右侧的小于 h 的最近元素的下标 right,如果不存在则为 n。求出了 right,那么 right−1 就是矩形最右边那根柱子。
比如示例 1(上图),选择 i=2 这个柱子作为矩形高,那么左边小于 heights[2]=5 的最近元素的下标为 left=1,右边小于 heights[2]=5 的最近元素的下标为 right=4。矩形的宽度就是 right−left−1=4−1−1=2,矩形面积为 h⋅(right−left−1)=5⋅2=10。
枚举 i,计算对应的矩形面积,更新答案的最大值。 如何快速计算 left 和 right?可以用单调栈。
var largestRectangleArea = function(heights) {
const n = heights.length;
const left = Array(n).fill(-1);
const st = [];
for (let i = 0; i < n; i++) {
const h = heights[i];
while (st.length && h <= heights[st[st.length - 1]]) {
st.pop();
}
if (st.length) {
left[i] = st[st.length - 1];
}
st.push(i);
}
const right = Array(n).fill(n);
st.length = 0;
for (let i = n - 1; i >= 0; i--) {
const h = heights[i];
while (st.length && h <= heights[st[st.length - 1]]) {
st.pop();
}
if (st.length) {
right[i] = st[st.length - 1];
}
st.push(i);
}
let ans = 0;
for (let i = 0; i < n; i++) {
ans = Math.max(ans, heights[i] * (right[i] - left[i] - 1));
}
return ans;
};